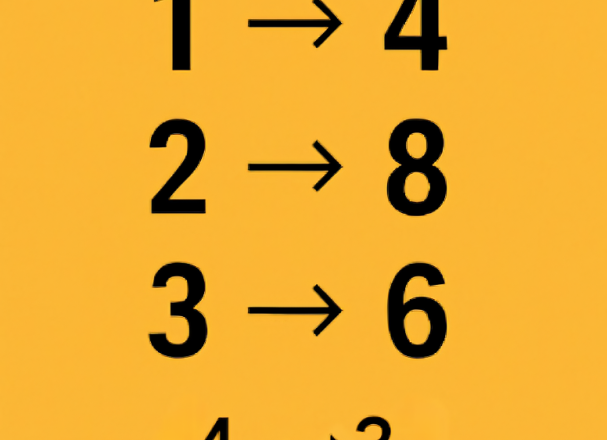
1 → 4
2 → 8
3 → 6
4 → ?

Na pierwszy rzut oka wydaje się, że to prosta arytmetyka, ale żeby dostrzec wzór, należy zwrócić uwagę na różnice i ich przemienność.

Dla 1 → 4: różnica 4 − 1 = 3

Dla 2 → 8: różnica 8 − 2 = 6

Dla 3 → 6: różnica 6 − 3 = 3

Uwaga: różnice wynoszą 3, 6, 3 . Wyraźnie widać, że są one naprzemienne: najpierw +3, potem +6, potem znów +3. Można założyć, że wzrośnie do +6.

Aby więc znaleźć odpowiedź na pytanie 4:

Bierzemy 4

Dodajemy kolejny krok, czyli 6

Otrzymujemy 4 + 6 = 10

Odpowiedź: 10

 Podpowiedź:
Zadania z naprzemiennymi krokami to klasyczna łamigłówka logiczna. Na pierwszy rzut oka nie jest oczywiste, dlaczego 2 staje się 8, a 3 6, ale jeśli zapiszesz różnice, wzór stanie się jasny: 3, 6, 3, 6… .

 Inny przykład:
Załóżmy, że masz sekwencję 5 → 9, 6 → 12, 7 → 10, 8 → ?

Różnice: 9 − 5 = 4, 12 − 6 = 6, 10 − 7 = 3

Kroki: 4, 6, 3 — również wykonuj naprzemiennie, a następny będzie nr 6, więc 8 + 6 = 14.

Ile czasu zajęło Ci znalezienie tego wzoru? Podzielcie się swoimi metodami i ulubionymi problemami logicznymi w komentarzach!